di Alessio Palmero Aprosio

Continua il racconto matematico in n puntate.

– È vero, basta risolvere l’equazione xy = 2x + 2y.
– Ti vedo sveglio. Quindi ti piacciono i giochi “a sfondo matematico”?
– Molto, ho anche partecipato alle Olimpiadi della Matematica.
– Allora ti propongo un quesito di “numerologia” e uno di “teoria dei numeri”…
– Ma come faccio a risolvere quello di numerologia?
– Vedrai che ce la fai… sarà finta numerologia.
– Proviamo, allora. – Andrea era un po’ spaventato, ma aveva capito che le sue passioni erano condivise anche da altre persone.
– Trovami l’unico numero di cinque cifre che gode della seguente proprietà: se gli metti un quattro davanti ottieni un numero che è esattamente quattro volte lo stesso numero con il quattro in fondo invece che all’inizio.
– E questo è quello di numerologia…
– Esatto! Per la teoria dei numeri devi dimostrarmi che per ogni numero primo maggiore di 4 vale la proprietà che [pmath]p^2 – 1[/pmath] è divisibile per 24.
– Certamente… però mi occorre una lavagna.
– Ehi, amico, piano con le richieste… diciamo che un foglio di carta sarà più che sufficiente. Andiamo in aula studio.
– Va bene, ma almeno prima mi dite come vi chiamate e se siete di matematica?
– Direi che questo almeno te lo sei meritato, ma prima dicci come ti chiami tu.
– Io sono Andrea e sono iscritto al primo anno di matematica.
– Devi sempre aggiungere informazioni inutili a quello che dici? Comunque io mi chiamo Luca e studio matematica, come te, ma al quarto anno, e questa non è un’informazione inutile perché non potevi saperlo. Loro sono Pietro e Carlo, del terzo anno di ingegneria.
– Ingegneria? Allora matematici e ingegneri non si odiano…
– Ma tu credi a tutto quello che dice il professore di analisi? Mi sa che ti credi già un po’ troppo “matematico”. Ti ricordo che sei al primo anno e hai ancora molte cose da imparare!
– Sì, forse hai ragione.
– Certo che ho ragione. – disse sorridendo – Ma andiamo in aula studio. Solo perché mi sei simpatico non vuol dire che ti risparmio le due dimostrazioni.
– Spero di riuscire a farle entrambe, tra venti minuti ho lezione.
– Che lezione hai?
– Geometria.
– Buona fortuna, allora. Comunque il fatto di riuscire o meno a fare le dimostrazioni dipende da te, a quanto sai essere preciso e conciso allo stesso tempo, anche se temo di no, vista la tua predilezione per le parole superflue.

Appena arrivati in aula studio i ragazzi si sedettero attorno ad un tavolo e Luca consegnò ad Andrea un foglio bianco.

di Alessio Palmero Aprosio

Continua il racconto matematico in n puntate.

Capitolo due

– Be’, mi sono segnato le quantità che ti ha detto. Se facciamo un diagrammino, – e disegnò un diagramma di Eulero-Venn – con i valori noti, vediamo che possiamo completarlo aggiungendo 2.601, 1.747 e 6.040. Guarda il disegno. Ora basta sommare tutti i numeri ed il gioco è fatto. Nella biblioteca ci sono 14.311 libri!

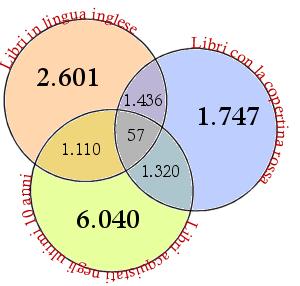
– È vero, non ci avevo pensato!
– Dai, è ora di andare, sono le nove… non vorrei sbagliarmi sul quarto d’ora accademico.
– Meglio non arrivare in ritardo, almeno il primo giorno. Avremo tempo di dormire domani e mercoledì, visto che iniziamo lezione alle 11.

I due tornarono davanti al Dipartimento. Giulia disse:

– Guarda, è arrivato qualcun altro.

In breve una piccola folla si era formata davanti all’entrata del Dipartimento di Matematica.
Per ultimo, alle nove e un quarto precise, arrivò il professore di analisi.

– Entrate pure, ragazzi, non siate timorosi.

Una volta in aula il professore iniziò la lezione.

– Buongiorno. Vi vedo molto numerosi… spero siate altrettanti l’ultima lezione.

Giulia sussurrò ad Andrea:

– Ma cosa sta dicendo? Perché dovremmo essere di meno? Dici che così tanti studenti rinunceranno a fare matematica?
– No, – rispose Andrea – non credo. Più che altro, visto che le lezioni non sono obbligatorie, molti studenti preferiranno rimanere a casa e studiare poi per conto loro.
– Dici davvero? Ma i professori non se la prendono se uno non va a lezione?
– Non credo più di tanto… in fondo li pagano lo stesso.

Il docente interruppe il discorso per riprendere i due che stavano chiacchierando:

– Ragazzi, almeno fate silenzio. Le lezioni non sono obbligatorie, quindi per venire e chiacchierare o leggere il giornale come fanno gli ingegneri statevene pure a casa vostra.
– Ci scusi, professore – disse Andrea.

L’insegnante continuò:

– Dove ero rimasto? Ah, sì. L’analisi. Vorrei fare una panoramica del corso, prima di iniziare a spiegare…

Il docente terminò la sua lezione, appoggiò il gesso sulla lavagna e salutò gli studenti.

– Arrivederci a domani, abbiamo lezione alle 11, non è vero?

Qualcuno dalla platea confermò e il professore finalmente lasciò l’aula.

– Ora ci dovrebbe essere lezione di geometria, o almeno dovrebbe essere alle 11. – disse Giulia.
– Credo che inizierà alle 11 e un quarto, quindi abbiamo mezz’ora di tempo.
– Già, ha anche finito un quarto d’ora prima.
– Mi sembra giusto, no? Ha fatto due ore da 45 minuti, che fanno un’ora e mezza, quindi i conti tornano.
– È vero, dovevo arrivarci: studio matematica! – e sorrise.
– Non è proprio la stessa cosa. Hai ascoltato quello che ha detto il professore di analisi? Non vedremo praticamente mai i numeri, ma più che altro studieremo in modo più profondo il perché delle cose… lasciamo i conti agli ingegneri!
– Vero. Quando uscirò di qui probabilmente dovrò chiedere aiuto per fare il conto della spesa!
– Non credo che arriveremo mai a tanto, dai… magari conosceremo un modo molto più veloce e comodo per calcolare la spesa senza dover impazzire con la calcolatrice…
– Credo che andrò a conoscere qualcun’altro nostro compagno di corso. Vieni anche tu?
– No, ho un leggero languorino. Ho visto una macchinetta del caffè nell’atrio, credo che conoscerò i nostri compagni più tardi.
– A dopo, allora.
– Ciao.

Andrea nel frattempo uscì dall’aula alla volta della macchinetta, trovando un gruppo di studenti che parlottavano. Uno di loro stava sorseggiando una bibita in lattina appena presa al distributore a fianco.

– Salve, ragazzi, anche voi di matematica?

I tipi si voltarono a guardare Andrea e non risposero.

– Sempre così simpatici? – e si avvicinò alla macchinetta del caffè.

Nel frattempo uno dei tizi si voltò verso Andrea:

– Hai dei problemi, matricola?
– Nessun problema. Potevate anche rispondere alla mia domanda.

Il ragazzo con la lattina si rivolse ad Andrea.

– Senti, saputello, ma voi di matematica siete tutti così?
– Così come?
– Una cerchia ristretta che si crede chissà chi…
– Io non credo niente, volevo solo fare conoscenza.
– A noi non interessa fare conoscenza con te, però…
– Beh, pazienza, non sai cosa ti perdi… – concluse Andrea peccando d’orgoglio.
– Senti, ragazzino, visto che sai tutto… facciamo che rispondi ad una domanda “a bruciapelo” – disse mimando le virgolette con le dita…
– Dimmi pure – rispose, senza dare a vedere troppo la sua agitazione.
– Allora, carissimo… sai qual è la differenza tra numerologia e teoria dei numeri?
– Più o meno la stessa che c’è tra astronomia e astrologia, – disse immediatamente, ma forse la numerologia è più interessante dell’astrologia: almeno non illude.
– Non male. E ora una domanda di cultura generale, che in un qualche modo riguarda anche la matematica. Perché il 17 porta sfortuna?
Andrea esitò un po’ dopo quella domanda, ma dopo qualche secondo, sicuro di sé, rispose:
– È una superstizione molto antica. In numeri romani il 17 si scrive XVII, anagramma di VIXI, cioè “vissi”, ovvero “sono morto”.
– Bravo ragazzo, non lo sapevo nemmeno io, e la tua risposta mi sembra molto ingegnosa, anche se non posso sapere se è quella giusta. Io ne conoscevo un’altra. Secondo i pitagorici il numero 17 portava sfortuna perché giaceva tra 16 e 18, gli unici due numeri interi che rappresentano aree di rettangoli a lati interi in cui il perimetro è uguale all’area.

Davvero?

di Alessio Palmero Aprosio

Continua il racconto matematico in n puntate.

Capitolo uno

– Ciao, io sono Andrea.

Andrea si era avvicinato a una ragazza che sembrava, come lui, in attesa. Entrambi sostavano davanti all’ingresso del Dipartimento di Matematica dell’Università.

– Anche tu iscritta a matematica? – proseguì lui.

La ragazza alzò lo sguardo un po’ spaventata e sorrise.

– Sì. Si vede tanto, eh? Mi chiamo Giulia. Mi fa piacere sapere di non essere l’unica persona iscritta a questo corso. Sei anche tu iscritto a matematica, immagino.
– Proprio così. Anche a me fa piacere non sentirmi solo. È da tanto che sei qui ad aspettare? Credo che le lezioni inizino alle undici e un quarto.
– Così tardi? Ma sul sito internet c’era scritto alle undici.
– Sì, ma c’è il quarto d’ora accademico.
– E che cosa è?
– Una sorta di “pausa”. In realtà le ore sono da 45 minuti, quindi la lezione inizia alle 9,15 e finisce alle 10.
– Ah, capisco, molto meglio all’inizio, il quarto d’ora, così si dorme un po’ di più. – e sorrise – Dovrebbero accantonare all’inizio tutte quelle della giornata, così dormiremmo un sacco in più. – disse per rompere il ghiaccio. E forse c’era anche riuscito – Di dove sei?
– Provincia di Verona, vivo qui in un appartamento. Tu di dove sei?
– Io di Mantova, non siamo molto distanti.
– Vero: una passeggiata. Che ne diresti di fare un giro nella biblioteca del Dipartimento? Sono solo le nove meno un quarto. Giusto per passare il tempo, così vediamo anche quanti libri ci sono dentro.
– Ma sì, dai: aspettare qui mi mette solo tensione.

La biblioteca era al secondo piano del Dipartimento. Appena entrarono videro un ragazzo che stava parlando con il bibliotecario.

– Mi saprebbe dire che giorno è oggi? – disse il ragazzo.
– Come sarebbe a dire… che giorno è oggi? – rispose il bibliotecario
– Sì, lunedì, martedì, mercoledì…

Il bibliotecario sorrise sotto i baffi e disse:

– Quando l’altro ieri era domani, oggi era distante da mercoledì come oggi sarà distante da mercoledì quando dopodomani sarà ieri.

Il ragazzo rimase sconvolto, e se ne andò a testa bassa.

– Ma come? Non ha nemmeno reagito? – disse Andrea
– Probabilmente sa che il bibliotecario è particolarmente… strano! – rispose Giulia
– Facciamo che allora lo chiedi tu il numero di libri che hanno?
– Perché dovrei farlo io?
– Perché lui è uomo e tu sei donna, sicuramente se lo dice a uno solo dei due, quell’uno sei tu.
– Forse hai ragione. Allora provo?
– Vai e distruggi! Al massimo usciremo di qui senza sapere quanti libri ci sono.

Giulia si diresse verso il bibliotecario, voltandosi di tanto in tanto verso Andrea, che la sosteneva moralmente.

– Buongiorno, – disse il bibliotecario – anche lei qui per una domanda stupida?
– N-no… sono una nuova iscritta a matematica e volevo solo chiederle quanti libri ci sono in questa biblioteca.
– Ma certo! E io sono qui per dare i numeri, vero?
– Non intendevo dire questo. – Giulia era già nel panico – Volevo solo chiedere un’informazione.
– Be’, se crede che io dia i numeri, allora li dò veramente. Le dico che 5.204 volumi sono in lingua inglese, 4.560 hanno la copertina rossa e 8.527 sono stati acquistati negli ultimi 10 anni. Inoltre 1.436 sono in inglese, hanno la copertina rossa, ma non sono degli ultimi 10 anni; 1.110 sono in inglese, acquistati negli ultimi 10 anni, ma non hanno la copertina rossa; 1.320 sono rossi, degli ultimi 10 anni, ma non in inglese; solamente 57 sono rossi, in inglese e sono stati acquistati negli ultimi 10 anni.

Giulia fece la stessa faccia del giovane di prima e ritornò da Andrea.

– Help! – disse lei

Andrea sorrise e aggiunse:

– Dai, in fondo è stato divertente, no?
– Per niente! – tuonò Giulia.
– E poi ho visto che si può calcolare quanti libri ci sono.
– E come fai?

Già, come fa? E, soprattutto: che giorno è?

di Alessio Palmero Aprosio

Pubblichiamo, da oggi ogni venerdì per n puntate (non vi dico quante sono: lo saprete solo alla fine), il racconto di alcuni ragazzi che si accingono a iscriversi all’Università. Ogni riferimento a persone, cose o numeri è puramente casuale.

Capitolo zero

Il candidato entrò dalla porta dell’aula, un po’ teso. La sala era grande, circa duecento posti, tutti rigorosamente vuoti. Andrea era l’unico di quella tiepida giornata di ottobre, l’unico e ultimo candidato di quell’ultimo appello di geometria prima dell’inizio delle lezioni del nuovo anno accademico. Entrò dalla porta posta sulla destra della lavagna; c’erano due porte per entrare nell’aula, una sulla destra e una sulla sinistra, una per gli studenti e una per i docenti, o almeno così diceva il regolamento.

Il docente:

– Il suo nome, prego.
– Davide Greco.
– È qui per l’esame di geometria, vero?
– Sì, secondo modulo.
– Beh, iniziamo in modo… standard. C’è un argomento del corso che le è piaciuto particolarmente?
– Così su due piedi…
– Non so, una parte del programma che l’ha colpita particolarmente.
– Spazi topologici.
– Bene, che cos’è uno spazio topologico?

Il giovane iniziò l’esposizione zoppicando un po’.

– Uno spazio topologico. Allora, dato uno spazio W, anzi no, dato un insieme X e una topologia tau…

Dopo circa 40 minuti l’orale stava volgendo al termine. Il candidato non era stato all’altezza della situazione, e il docente sarebbe dovuto andare, di lì a poco, a svolgere la prima lezione del nuovo anno accademico ai nuovi iscritti.

– Mi disegni una retta.

Il candidato tracciò una linea sulla lavagna.

– Non ci siamo, mi dia la definizione euclidea di retta.
– Una retta è una linea infinita.
– Meglio definita come lunghezza senza larghezza, non è così?
– Be’, sì…
– E le sembra lunghezza senza larghezza? Quello è un segmento, non una retta.

Il candidato allungò la linea fino al bordo della lavagna.

– Prosegua pure sul muro.

Così fece.

– Vada pure avanti, fuori dalla porta.

Così dicendo il candidato uscì dalla porta sulla destra della lavagna, e il docente da quella sulla sinistra.

(continua)